Princip šifrování
Z MiS
(Rozdíly mezi verzemi)
(→Související stránky: Přidán odkaz na Certifikační autorita.) |
(→Zajímavost — historické šifry: Přidány příklady historických šifer.) |
||
| Řádka 89: | Řádka 89: | ||
== Zajímavost — historické šifry == | == Zajímavost — historické šifry == | ||
* Césarova šifra (přelom letopočtu): [https://www.algoritmy.net/article/34/Caesarova-sifra Algoritmy.net → Caesarova šifra] | * Césarova šifra (přelom letopočtu): [https://www.algoritmy.net/article/34/Caesarova-sifra Algoritmy.net → Caesarova šifra] | ||
| + | ** Každé písmenko zprávy posunete o zadaný počet písmen v abecedě. | ||
| + | ** Klíčem je zde počet písmen, o které posunujeme. | ||
| + | <div class="Priklad">Příklad: <code>A h o j K a r l e</code> + klíč <code>2</code> → <code>C j q l M c t n g</code></div> | ||
* Vigenèrova šifra (1556): [https://www.algoritmy.net/article/53/Vigenerova-sifra Algoritmy.net → Vigenèrova šifra] | * Vigenèrova šifra (1556): [https://www.algoritmy.net/article/53/Vigenerova-sifra Algoritmy.net → Vigenèrova šifra] | ||
* Šifra Playfair (1854): [http://www.shaman.cz/sifrovani/sifra-playfair.htm Shaman.cz → Šifra Playfair] | * Šifra Playfair (1854): [http://www.shaman.cz/sifrovani/sifra-playfair.htm Shaman.cz → Šifra Playfair] | ||
* Vernamova šifra (1917): [https://cs.wikipedia.org/wiki/Vernamova_%C5%A1ifra Wikipedia.org → Vernamova šifra] | * Vernamova šifra (1917): [https://cs.wikipedia.org/wiki/Vernamova_%C5%A1ifra Wikipedia.org → Vernamova šifra] | ||
| − | ** | + | ** Vlastně podobný princip jako Césarova šifra, ale každé písmeno zprávy posunu o jiný počet znaků. |
| − | ** Důkaz neprolomitelnosti Shannon 1949. | + | ** Klíčem je informace, které písmeno posunout o kolik znaků. |
| + | ** Reálně bychom brali datový soubor se zprávou a ke každému byte zprávy přičítali odpovídající byte z náhodně vygenerovaného klíče. | ||
| + | ** Je neprolomitelná, pokud dodržíme pravidla: 1) klíč stejně dlouhý jako zpráva a 2) klíč je dokonale náhodný. | ||
| + | ** Důkaz neprolomitelnosti podal Shannon v roce 1949. | ||
| + | ** Problém je ale s předáním klíče. | ||
| + | <div class="Priklad">Příklad: <code>A h o j K a r l e</code> + klíč <code>2 3 1 4 3 2 5 4 1</code> → <code>C k p n M c w p f</code></div> | ||
* Enigma (1918) | * Enigma (1918) | ||
** Originální verze prolomena už ve 30. letech 20. století. | ** Originální verze prolomena už ve 30. letech 20. století. | ||
| Řádka 99: | Řádka 107: | ||
** K prolomení byly používány výpočetní stroje (předchůdci počítačů), na jejich vývoji se podílel Alan Turing. | ** K prolomení byly používány výpočetní stroje (předchůdci počítačů), na jejich vývoji se podílel Alan Turing. | ||
| + | ; Úkol | ||
<div class="Ukol"> | <div class="Ukol"> | ||
; Vyzkoušejte si šifru Playfair: | ; Vyzkoušejte si šifru Playfair: | ||
Verze z 7. 6. 2018, 09:46
Obsah |
Rozdělení šifrovacích metod
- Symetrické šifrovací metody
- Odesilatel i příjemce mají společný šifrovací klíč.
- Společným šifrovacím klíčem lze zprávu zašifrovat i dešifrovat.
- Asymetrické šifrovací metody
- Účastník je identifikován dvojicí klíčů
- soukromý klíč: zná pouze vlastník
- veřejný klíč: smí znát kdokoli
- Postupným použitím soukromého i veřejného klíče dostaneme původní zprávu.
- Zpráva zašifrovaná veřejným klíčem lze dešifrovat pouze soukromým klíčem a naopak.
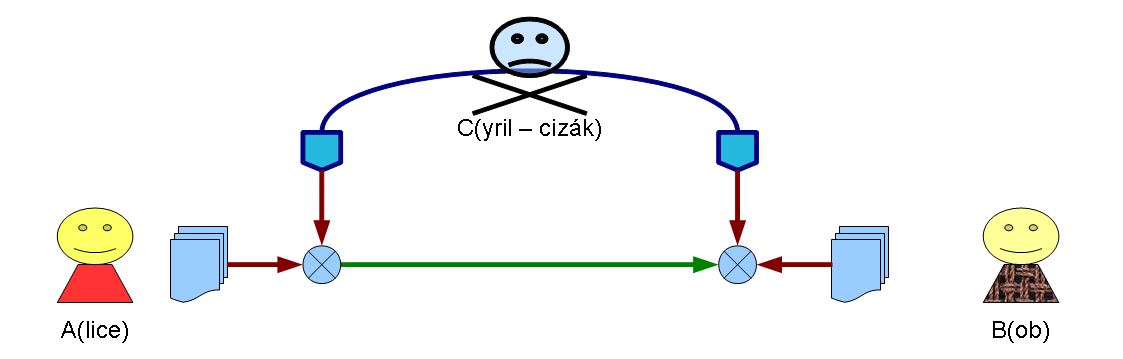
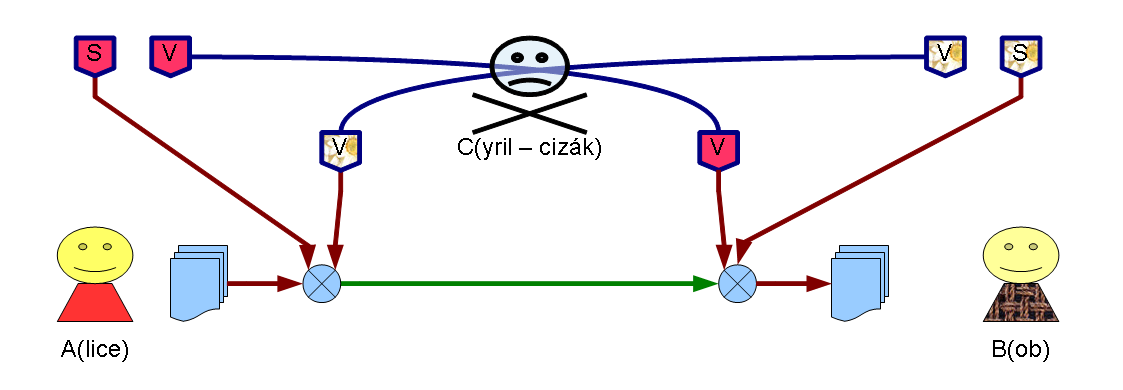
Šifrování symetrickou šifrovací metodou
- Odesilatel i příjemce mají společný šifrovací klíč, kterým lze správu zašifrovat i rozšifrovat.
- Při komunikaci na dálku vzniká problém s předáním šifrovacího klíče (pokud se odesilatel a příjemce nemohou sejít osobně předem)!
- Klíč by měl být dostatečně dlouhý a náhodný.
- Klíč by měl být použit pouze jednou!
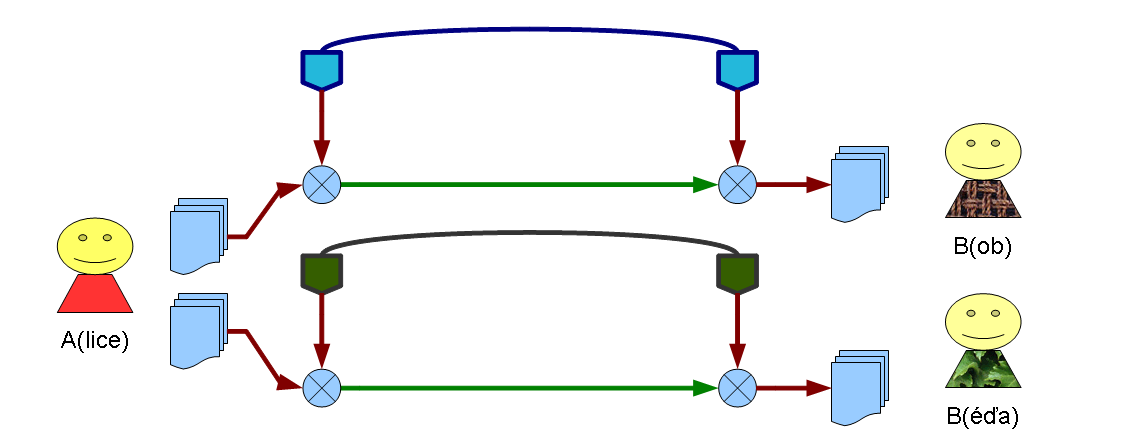
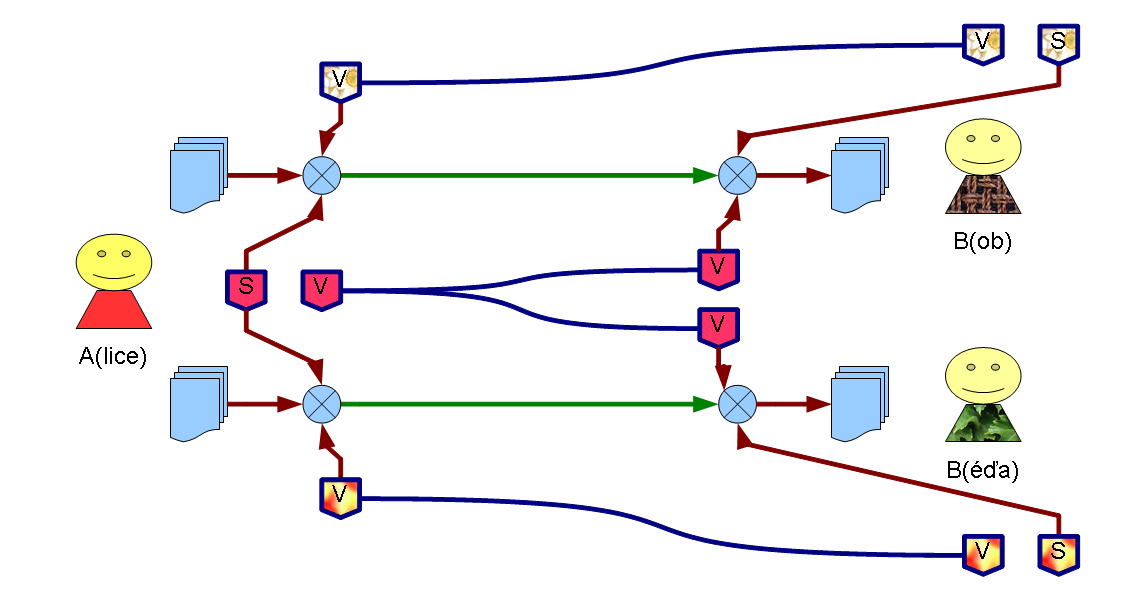
Šifrování asymetrickou šifrovací metodou
- Každý účastník komunikace má pár veřejný + soukromý klíč.
- Odesilatel si nechává svůj soukromý klíč, ten nikomu nesděluje.
- Veřejný klíč může znát kdokoli, případné přečtení při předávání veřejnou sítí tedy není rizikem.
Běžné využití
- Asymetrické šifrovací metody jsou obvykle využívány pro bezpečné předání symetrického šifrovacího klíče nebo otisku zprávy.
- Šifrování většího objemu dat se obvykle následně provádí symetrickými šifrovacími metodami.
- SSL
- Vrstva pro šifrovanou komunikaci (implementace části prezentační vrstvy).
- Předchůdce protokol TLS
- Typicky se používá pro šifrovaný přenos dat protokolu HTTP (https://...).
- Viz také: Secure Sockets Layer
Porovnání vlastností
Asymetrické šifrovací metody:
- Dokáží zajistit nepopiratelnost odeslání zprávy.
- Autor zprávy nemůže popřít její odeslání.
- Ulehčují problém s bezpečným předáním klíče potenciálně nebezpečnou sítí.
- Nevadí odposlechnutí klíče třetí osobou, je jen třeba zabránit podvržení falešného klíče.
- Jedna kombinace veřejného a soukromého klíče stačí pro komunikaci s libovolným počtem partnerů.
- Každý účastník zodpovídá za svůj soukromý klíč, není zde sdílená zodpovědnost za vyzrazení klíče.
Symetrické šifrovací metody:
- Jsou výpočetně méně náročné.
Příklady šifrovacích algoritmů
Symetrické šifrovací algoritmy
- DES
- Data Encryption Standard
- Délka klíče 56 bitů, dnes již nedostatečné vzhledem k výkonu dnešních počítačů!
- AES
- Advanced Encryption Standard, nebo také Rijndael [rendál]
- Autoři: Joad Daemen, Vincent Rijmen
- V roce 2001 přijat americkým Národním institutem pro standardizaci a technologie (NIST) jako standard pro šifrování vládních dokumentů (odtud AES).
- Délka klíče: 128, 192, nebo 256 bitů (u původního algoritmu Rijndael lze libovolně prodloužit)
- Bloková šifra (CBC - Cipher Block Chaining)
- další blok se XOR-uje předchozím a pak až šifruje
- generujeme náhodný 0. blok, kterým jen XOR-ujeme první.
- Serpent
- Autoři: Ross Anderson, Eli Biham a Lars Knudsen
- Náročnější na implementaci než Rijndael pro malé bloky (32 kol)
- Není patentována, je public domain.
- Druhá metoda ve finále volby AES spolu s vítěznou Rijndael.
- Zdroje: Wikipedia.org: Serpent (cipher)
- Twofish
Asymetrické šifrovací algoritmy
- RSA
- Autoři: Rivest, Shamir, Adleman
- Je základem protokolu SSL.
- Matematický princip: Malá Fermatova věta (násobení velkých prvočísel)
Zajímavost — historické šifry
- Césarova šifra (přelom letopočtu): Algoritmy.net → Caesarova šifra
- Každé písmenko zprávy posunete o zadaný počet písmen v abecedě.
- Klíčem je zde počet písmen, o které posunujeme.
Příklad:
A h o j K a r l e + klíč 2 → C j q l M c t n g- Vigenèrova šifra (1556): Algoritmy.net → Vigenèrova šifra
- Šifra Playfair (1854): Shaman.cz → Šifra Playfair
- Vernamova šifra (1917): Wikipedia.org → Vernamova šifra
- Vlastně podobný princip jako Césarova šifra, ale každé písmeno zprávy posunu o jiný počet znaků.
- Klíčem je informace, které písmeno posunout o kolik znaků.
- Reálně bychom brali datový soubor se zprávou a ke každému byte zprávy přičítali odpovídající byte z náhodně vygenerovaného klíče.
- Je neprolomitelná, pokud dodržíme pravidla: 1) klíč stejně dlouhý jako zpráva a 2) klíč je dokonale náhodný.
- Důkaz neprolomitelnosti podal Shannon v roce 1949.
- Problém je ale s předáním klíče.
Příklad:
A h o j K a r l e + klíč 2 3 1 4 3 2 5 4 1 → C k p n M c w p f- Enigma (1918)
- Originální verze prolomena už ve 30. letech 20. století.
- Prolomení pokročilejší verze šifry pomohlo vítězství ve 2. světové válce.
- K prolomení byly používány výpočetní stroje (předchůdci počítačů), na jejich vývoji se podílel Alan Turing.
- Úkol
- Vyzkoušejte si šifru Playfair
Chcete-li vyzkoušejte si šifrování šifrou Playfair. Zkuste zakódovat text:
Šifruji jako blesk!
Pomocí klíče:
Informatika
Řešení — výsledný šifrovaný text by měl znít:
Looíl Rf, vnmg. Kmú gqbý.
(Interpunkce, diakritika a velikost písmen jsou přidány náhodně.)